奔向赛场:一种通用元策略
利用简单概念实时选择表现最佳的交易策略
作者:Paper to Profit | 发布日期:2025年6月3日

1821年Epsom赛马会。我想当时这些人并未考虑优化算法交易策略组合。
我们经常会有一篮子资产,并将其转化为交易策略。但同样,我们也有一篮子交易策略,需要将资金分配其中。在上一篇文章中,我展示了如何利用生成式AI创造理论上无限多的交易策略。然而,如果这些策略无法盈利,这一切就毫无意义。
回测可以告诉我们过去发生了什么,但这会引入数据窥探(data snooping)的问题。一个元策略(metastrategy),即一个自适应系统,能够为我们选择最佳系统,是一个更好的解决方案。我基于深入研究开发了一个定制算法,使我们非常接近最佳策略的表现,或者说接近理论上的超额表现。
工作原理如下:
与其一直分析所有系统,我更倾向于让表现好的策略自己告诉我谁是赢家。就像赛马一样,我让这些策略在赛道上‘奔跑’,在途中观察哪些策略领先。尽管这看似非常简单,但它的有效性却出人意料。
视觉示例
请观看以下视频:
你看到的是100个随机策略,它们的表现是随机生成的百分比收益和损失。当它们的最高净值增加时,它们会沿着赛道向终点线移动。因此,当某条线不动时,说明该策略正处于回撤期。黑线突出显示了每一阶段的前10名表现者。
请注意一个奇怪的现象:尽管这些策略只是随机噪声,但在比赛进行到一半时,当前的领先者变化不大,他们继续保持领先。而落后的策略则一直滞后,无所贡献。
这就是我用于开发通用元策略的相同概念。我让比赛继续进行,但使用的是真实策略,然后在一定时间后,选择表现最佳的策略并只投注于它们。就像让市场为我决定谁是赢家。
一个简单应用
在我的上一篇博客中,我生成了164个稳健的策略,每个策略有8种配置(4个窗口回溯期 × 2个再平衡周期)。为了去掉人工干预部分,我回到了最初的259个策略组合,并计算了259 × 8个策略的回报(去掉2个后共计2070个)。
然后,我定义了一个‘燃烧’周期(burn rate),即我们让策略运行一段时间后选择最佳专家的时间。让策略运行更长时间可以让表现不佳的策略有更多机会被淘汰。
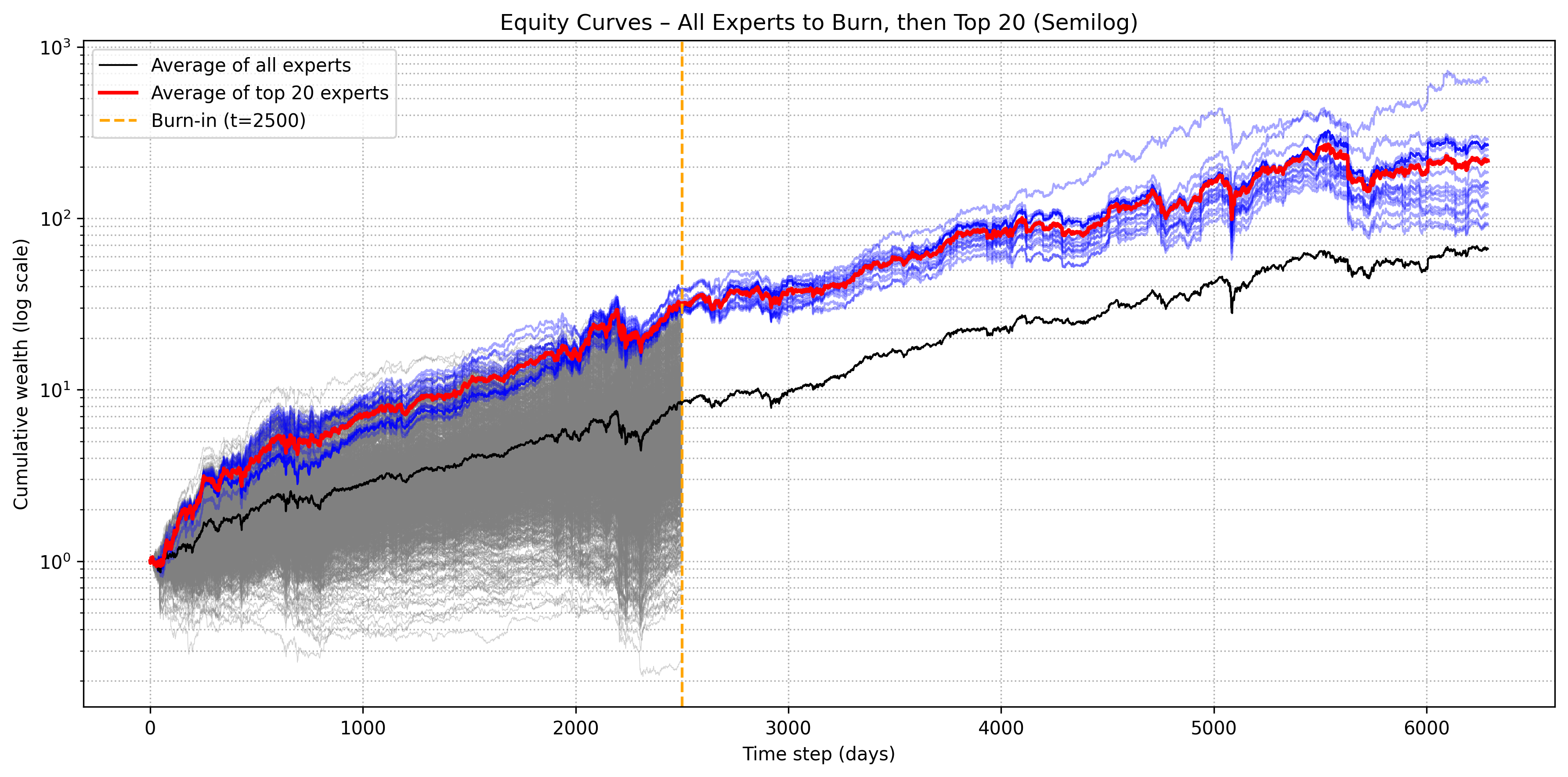
以上是这一过程。我在所有2070个策略运行2500天后选择了前20名专家。之后,仅投资于这前20名(等权重)。你可以看到该元策略的表现与所有系统等权重的元策略相比如何。
现在,我们需要建立一些基准指标,以了解这种方法的整体表现如何。
我们可以假设最差的元策略表现等同于所有策略的等权重组合,因为这是最朴素的选择。最佳元策略则是从第一天就投资于最优策略,因为我们无法赚取比这更多的钱*。
*我们可以,但我这次不打算深入探讨。
无论如何,以下是设置1000天‘燃烧’周期,然后筛选出前20个资产并等权重投资于所有20个资产的情况:
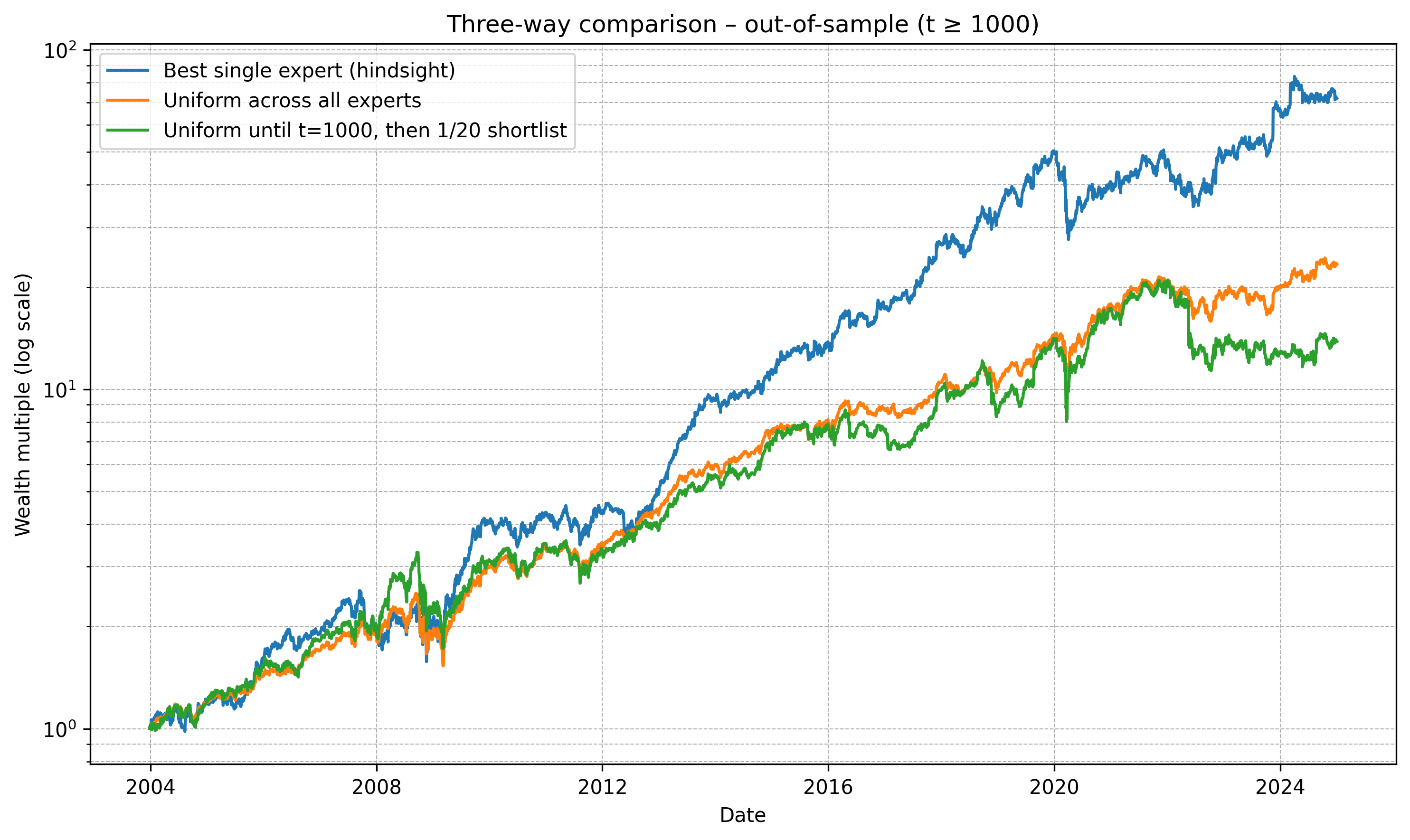
财富倍数 (t ≥ 1000)
最佳单一专家 (事后视角) : 71.94×
所有专家等权重 : 23.34×
t=1000前等权重,然后筛选1/20 : 13.82×
哇,这个策略表现太差了。它的表现比我们对所有2070个策略等权重投资还要糟糕。这时我意识到,或许我可爱的小马秀概念已经彻底失败了。直到我考虑了另一件事:
为什么要在所有顶级策略上等权重投资,我们明明知道它们的表现会有起伏?某些策略在某些时间段表现会优于其他。
因此,我的策略的压轴之作应运而生。
实时投注‘赛马’
是的,我遇到了一点小挫折。但这永远不会阻止我实现目标。如果我们知道策略的表现有起有伏,坚持一个前k名的等权重元策略毫无意义。
我设计了一个简单的轮换系统,流程如下:
- 每75天计算前一季度我们筛选出的前k名策略中哪个表现最好。
- 将资金100%分配到该系统,并在下一季度持有。
这允许一定的适应性,而不会因大规模轮换而影响表现。
我还应该提醒你,这2070个策略高度相关,它们的投资组合中包含相同的10-12个资产。这也使得设计元策略变得更加困难,因为所有策略相似,缺乏真正的非相关‘对冲’。我将在下一步研究多样化。
结果
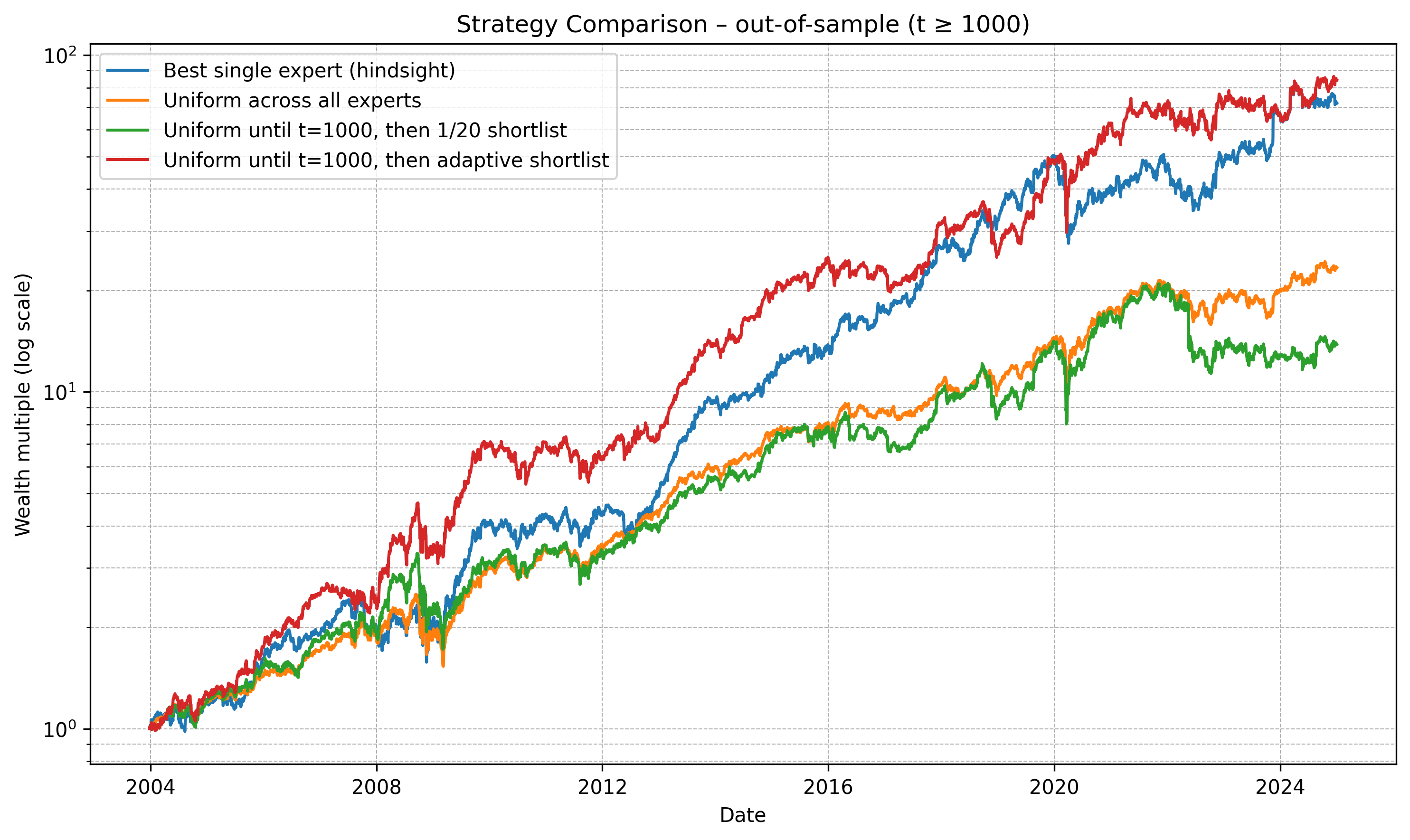
财富倍数 (t ≥ 1000)
最佳单一专家 (事后视角) : 71.94×
所有专家等权重 : 23.34×
t=1000前等权重,然后筛选1/20 : 13.82×
t=1000前等权重,然后适应性筛选 : 84.15×
现在我们看到了惊人的表现。一点小小的适应性让我们的元策略能够在没有前瞻性知识的情况下与事后最佳专家竞争并超越其表现。这是好消息,意味着我们可以通过结合表现追踪和适应性,追踪最佳专家并期望接近的表现。
自行实施
你可以通过简单地将策略回报矩阵导入系统,自行试验这些算法。
祝研究愉快!
发表回复