此博客是系统化的
同时也是自动化、流体化的:”极客启迪” Rob Carver关于量化交易、投资和经济学的博客。
2025年6月2日,星期一
快速文章 #1:过拟合与 EWMAC 预测标量
我现在正全力投入书籍写作,因此没有时间撰写完整的博文。相反,我计划发布一系列快速文章,分享我为书做的一些研究。说得有点 cynical,这也有可能促使您购买这本书,只要我不过度分享,就像那些泄露情节并包含所有精彩动作场景的电影预告片一样。
过拟合 – 图文指南
这是我经常使用的一张幻灯片:
尽管我们直观地知道复杂性可以提高样本内表现,但到了某个点会使其变得更糟,我们能将其可视化吗?
假设我认为过去64个交易日的涨跌模式能预测下一个月(大约20个交易日)的收益。我可以通过以下方式分析这些模式:
- 使用一个周期:只查看过去64天的交易,看价格是上涨还是下跌。由于周末和假期,这大约是三个月。
- 使用两个周期:查看前32天和后32天的交易。现在您明白我为什么使用64天了。
- 四个周期:检查前16天、第二个16天、第三个16天,然后是最后16天。
理论上,我最终可以每天单独查看,但实际上,我将在16个为期四天的周期时停止,这被证明足够有趣(对于四个周期,有2^4 = 16种可能的状态,而2^64简直是荒谬)。对于我的分析,我查看市场在每种日收益模式之后平均表现如何。例如,如果我使用两个32天收益来形成我的模式,那么有四种可能性:上涨和上涨、上涨和下跌、下跌和上涨;以及下跌和下跌。然后我可以看到市场在每种这四种状态下,20天后是上涨还是下跌。
随后,为了用这种方法进行交易,我将计算市场当前所处的状态,如果该状态在过去导致市场上涨幅度超过平均水平,我就会买入。这是一个单边做多的投资组合,因此如果我预期市场会下跌超过平均水平,我不能做空。相反,我只会保持空仓。
该图显示了对 Microsoft 执行此操作的结果。我几乎可以使用任何工具得到相同的图像——这是不需要大量数据池也能获得稳健结果的情况之一。
不幸的是,我们无法真正实现这些高水平的利润。问题在于我们正在样本内拟合该方法到所有可用的价格历史。因此,我们现在按照通常的程序进行样本外测试:将该方法拟合到数据的较早部分,然后对较晚的数据周期测试该校准后的方法。请注意,我们可能会看到以前从未见过的状态,在这种情况下,我们会从最后已知状态向前填充。
让我们看看如果我使用16个为期四天的周期,在2015年之前的全部历史数据上拟合我的方法,然后用后十年测试它,会发生什么。
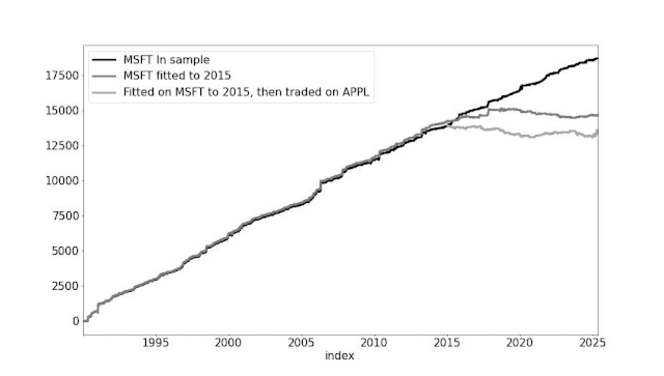
黑线使用的是原始程序;我们获取所有价格历史并相应地校准我们的方法。它的表现非常好,但正如我前面指出的,这在现实中是无法实现的。深灰色线只拟合到2015年初。在此之前,它的表现与黑线非常相似,这并不奇怪,因为这两种方法几乎相同,并且共享大约70%用于拟合的数据。
然而,2015年之后,当它根据从未见过的价格历史进行交易时,其表现急剧恶化。另一个有用的实验是,看看该方法在不同工具上的表现如何。浅灰色线显示了如果使用2015年的 Microsoft 方法随后交易 Apple (AAPL) 会发生什么。您可以清楚地看到其表现非常糟糕。这种方法与2015年之前的 Microsoft 收益拟合得过于紧密;它在后期年份表现不佳,特别是对于不同的股票。
如果我对一个更简单的模型执行相同的程序,仅仅查看整个64天周期会发生什么?由于我们知道股票价格在几个月内会呈现趋势,我们已经可以猜测这种拟合方法会是什么样子。如果价格在过去64天上涨,它就会买入,否则它不会做任何事情。
如图所示,无论拟合方法是根据到2015年的价格历史构建,还是根据整个时期构建,其最终结果都完全相同。因此,深灰色线与黑线完全重叠。您还可以看到,这种非常简单的方法在它以前从未见过的 Apple 股票上表现非常好。
计算而非测量 EWMAC 的预测标量
我以前的书籍中包含了各种交易规则的预测标量估计值。其中许多遵循时间平方根法则。例如,使用每日收益标准差进行归一化的 EWMACN, 4N 的标量,对于2,8大约是15,对于4,16大约是10,依此类推。我们通过除以 sqrt(2) 来得到下一个标量。一旦你估计了2,8,你就可以轻松推导出其他数字。
这很棒,但是除了2,8之外,我们如何获得不同起始乘数的“种子”值呢?我首先生成了一个所有2的幂的乘数完整表格:

行是 fast,列是 slow。由于对于趋势跟踪来说 fast<slow,所以底部对角线是空的。我们需要计算顶行中的数字。请注意,这对于任何 S EWMAC 2,S 的值也应该有效;但在2的幂空间中进行拟合更容易。
我使用了…… ChatGPT!是的,我只是把这些数字粘贴进去,然后让它进行拟合。它使用了幂律分布,当我要求它包含一个截距时,它甚至给了我所需的 Python 代码。这不是一个完美的拟合,因为是经验数据,但正如我的书中的脚注所说,所有这些努力都是为了:
对于 f=2 和给定值 s,使用公式 2.2+(184÷s^1.25) 计算相应的缩放因子。
随着 S 值越来越长,拟合效果会逐渐变差,但这也很合理,因为收益的长期偏差等因素往往会产生更大的影响。
发布者:Rob Carver (永久链接)
通过电子邮件发送 | 发布到博客 | 分享到 X | 分享到 Facebook | 分享到 Pinterest
暂无评论:
发表评论
评论会经过审核。因此,发布会有延迟。请勿发布垃圾信息,这会浪费您的时间和我的时间。
订阅:所有评论 (Atom)



发表回复