Trading the Breaking Data: Range, Renko, Filter and Volatility bars [+CODE INSIDE]

数据：Range、Renko、Filter和Volatility bars [+代码示例]

金融Bar之二

2025年6月2日

Trading the Breaking Data: Range, Renko, Filter and Volatility bars [+CODE INSIDE]

引言
时间Bar的风险与局限性
信息驱动型Bar介绍
Range bars（区间Bar）
Renko bars（Renko Bar）
Filter bars（过滤Bar）
Volatility bars（波动率Bar）

引言

您正在实时观察市场——成千上万个价格跳动（tick）在屏幕上涌现，每个跳动都反映了供需和市场情绪的瞬间转变。乍一看，数据似乎均匀分布、结构规整。然而，在这表面之下隐藏着更深层次的不对称性：市场活动的节奏并非由时钟的均匀节拍所控制，而是由信息流和波动性的不规则脉冲所驱动。

这种区别凸显了金融数据采样的一个根本挑战：即时间性时间与更恰当称为市场时间之间的不协调。传统的时间Bar——例如1分钟或5分钟的间隔——虽然提供了简单性并与标准回测框架兼容，但它们假设每个时间单位都具有相同的信息权重。然而，现实远比这复杂得多。

市场是事件驱动的。活动和波动性并非均匀分布。低流动性午间平静期的5分钟间隔与中央银行公告期间的5分钟窗口不等同。然而，两者在基于时间的采样中被同等对待。这可能导致误导性信号，特别是对于对波动率状态或订单流敏感的策略。

此外，时间Bar会带来众所周知的统计学复杂性。波动率聚集（Volatility clustering）导致极端变动时期与平静时期在相同的时间单位（temporal units）中被聚合，产生对风险模型、信号生成算法和机器学习（machine learning）架构性能造成损害的异方差收益序列。例如，尝试在这种信息不均匀的数据上训练预测模型可能会产生不稳定或过度拟合的结果。

其他方法，如Tick Bar、成交量Bar（volume bars）和美元Bar（dollar bars），旨在通过根据市场活动而非流逝时间重新定义采样来解决这些缺点。Tick Bar将固定数量的交易分组，适应市场参与的爆发。成交量Bar聚合数据直到固定数量的股票或合约易手。美元Bar更进一步，通过基于名义交易价值进行聚合，在不同交易工具之间进行标准化。这些方法通常会产生更具统计稳定性的回报，并更好地与市场信息流保持一致。有关这些Bar的更多信息，请参阅此处：

𝚃𝚛𝚊𝚍𝚒𝚗𝚐 𝚝𝚑𝚎 𝙱𝚛𝚎𝚊𝚔𝚒𝚗𝚐 Data: Financial bars [+CODE INSIDE] 阅读更多 7 天前 · 7 赞 · 𝚀𝚞𝚊𝚗𝚝 𝙱𝚎𝚌𝚔𝚖𝚊𝚗

最终，选择合适的采样方法并非出于便利——它是一个设计决策，决定着交易策略的行为、准确性和稳健性。尽管基于时间的Bar仍然普遍，但其局限性不容忽视。今天我们将审视一种完全不同类型的Bar，其中一些在交易者中相当常见和流行。

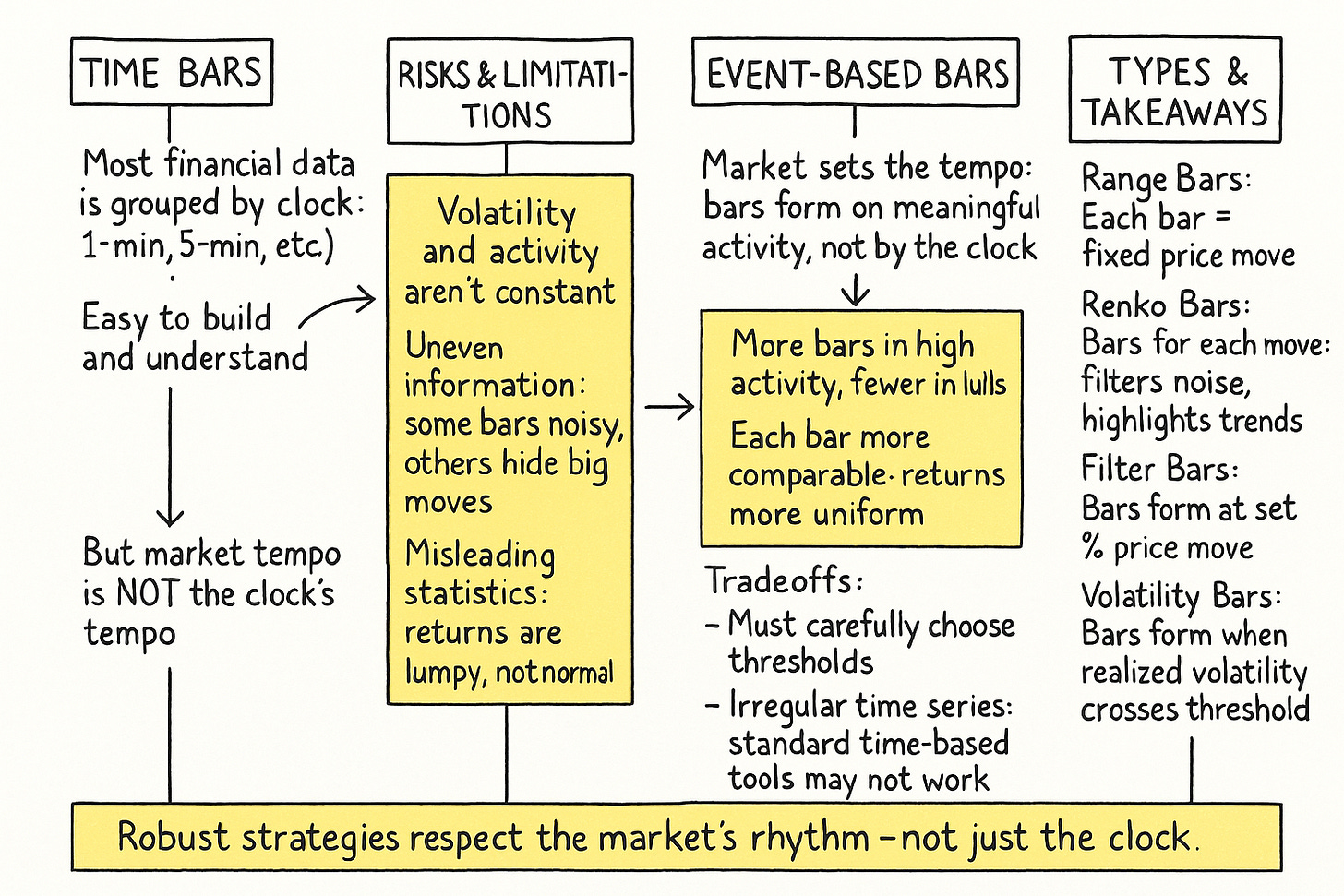
时间Bar的风险与局限性

超越基于时间的Bar，是为了寻求一种更智能的市场时钟，它不是随秒针流逝而跳动，而是随有意义事件的发生而跳动。其理念是，不根据时钟规定进行观察采样，而是当市场出现一些有趣的事情时进行。这引出了信息驱动型Bar的概念，其中每个Bar代表着一致的信息量，无论这些信息量如何定义——某个价格变动、特定的交易量成交，抑或特定数量的资本易手。

但这条道路并非阳光普照的草地；它是一个迷宫，充满了重重障碍。这些Bar的灵活性带来吸引力的同时，也引入了复杂性。

价格变动多大才能构成“有意义的事件”？
价格变化的“砖块”应该有多大？
何种程度的波动性需要形成新的Bar？

这些问题将量化交易者（algorithmic trader）推入参数选择的浑水，这是一个过度拟合的警报声不断响起领域。此外，这些Bar在时钟时间上的不规则出现，使得传统的时间序列分析（time-series analysis）技术难以直接应用，需要对持续时间（duration）和季节性（seasonality）等概念采取新的视角。

传统的基于时间的Bar——例如1分钟、1小时——是历史默认选项。它们以固定的时间间隔对价格数据进行采样。尽管计算和理解简单，但其核心缺陷在于假设市场活动在时间上均匀分布。这显然是错误的。市场表现出活动活跃和不活跃的时期，而基于时间的Bar对这些时期一视同仁。

以两个5分钟的Bar为例：

Bar A (低活动量): 价格在狭窄范围内波动。这个Bar捕捉到的信息量极少，可能只是噪音。
Bar B (高活动量): 新闻事件导致价格飙升和暴跌。这个Bar捕捉到了显著的趋势和波动性，但却将其塞进了与Bar A相同的时间框内。

这种差异导致算法模型出现以下几个问题：

归因（Returns）的方差在Bar之间并非恒定。假设同方差性的统计模型将会被错误设定。
基于时间的Bar的收益分布通常表现出过度的峰度（excess kurtosis）——厚尾——和偏度，偏离了许多金融模型所假设的正态分布。
在低活动量时期，时间Bar会累积噪音。在高活动量时期，固定间隔内的关键日内细节可能会丢失或被平均化。

这种错觉在于我们以为在衡量市场；而实际上，我们常常只是在衡量时钟，将市场行为强行纳入任意的时间网格。因此，我们的目标是寻找能适应市场节奏而非外部节奏的采样方法。

信息驱动型Bar介绍

信息驱动型Bar，或事件驱动型Bar，是根据信息流而非时间的流逝构建的——这里重要的是我们如何定义信息。目标是创建每个Bar都代表相似“市场事件量”的Bar，这种同步性旨在生成具有更理想统计特性的Bar序列，例如更接近独立同分布（IID）的收益，并且理想情况下更接近正态分布。

其基本前提是，重要的市场事件——价格变化、交易量激增、波动率飙升——才是真正重要的。通过基于这些事件形成Bar，我们让市场本身决定采样频率。当市场活跃时，Bar会迅速形成，捕捉市场动态。当市场平静时，Bar会缓慢形成，耐心等待有意义的信息。这种动态采样是价格变动的Bar的显著特征。

以下 Python 代码片段概述了由 Hudson and Thames 公司开发的基类结构，我们将使用它来构建所有Bar。此外，它还可以用于实现各种类型的信息驱动型工具栏（toolbars），而不仅仅是 López de Prado 推广的那些。这展示了在引入特定事件触发器之前的一种通用框架。

from abc import ABC, abstractmethod
import pandas as pd
import numpy as np
from collections import deque

def _batch_chunks(df, size):
        """
    Split DataFrame into equal-sized chunks for batch processing.
    """
    idx = np.arange(len(df)) // size
    return [grp for _, grp in df.groupby(idx)]


class BaseBars(ABC):
    def __init__(self, metric=None, batch_size=int(2e7)):
        self.metric = metric
        self.batch_size = batch_size
        self.reset()

    def reset(self):
        self.open = self.high = self.low = self.close = None
        self.prev_price = None
        self.tick_rule = 0
        self.stats = dict(cum_ticks=0, cum_dollar=0, cum_vol=0, cum_buy_vol=0)

    def _sign(self, price):
        if self.prev_price is None:
            diff = 0
        else:
            diff = price - self.prev_price
        self.prev_price = price
        if diff != 0:
            self.tick_rule = np.sign(diff)
        return self.tick_rule

    def run(self, rows):
        bars = []
        for t, p, v in rows:
            self.stats['cum_ticks'] += 1
            self.stats['cum_dollar'] += p * v
            self.stats['cum_vol'] += v
            if self._sign(p) > 0:
                self.stats['cum_buy_vol'] += v
            # initialize OHLC
            if self.open is None:
                self.open = self.high = self.low = p
            # update
            self.high = max(self.high, p)
            self.low = min(self.low, p)
            self.close = p
            # check threshold
            self._check_bar(t, p, bars)
        return bars

    def batch_run(self, data, to_csv=False, out=None):
        cols = ['date', 'tick', 'open', 'high', 'low', 'close',
                'vol', 'buy_vol', 'ticks', 'dollar']
        bars = []
        if isinstance(data, pd.DataFrame):
            chunks = _batch_chunks(data, self.batch_size)
        else:
            chunks = pd.read_csv(data, chunksize=self.batch_size, parse_dates=[0])
        for chunk in chunks:
            bars.extend(self.run(chunk[['date', 'price', 'volume']].values))
        df = pd.DataFrame(bars, columns=cols)
        df['date'] = pd.to_datetime(df['date'])
        df.set_index('date', inplace=True)
        if to_csv and out:
            df.to_csv(out)
        return df

    @abstractmethod
    def _check_bar(self, t, p, bars):
        ...

这个 BaseBars 类巧妙地提供了一个用于累积 Tick 数据的通用引擎，并将何时形成Bar的关键决策委托给其子类。这是设计我们自己的市场时钟的开端。

Range bars（区间Bar）

Range bars（区间Bar）是概念上最简单的价格变动型Bar之一。当价格区间（高点 – 低点，或更常见的是正在形成的Bar的 |收盘价 – 开盘价|）超过预设阈值 R 时，就会形成一个新的Bar。

\(\text{close when}\;\bigl|\mathrm{close}_i – \mathrm{open}_k\bigr| \ge R \)

其中 _open k_ 是当前正在构建的Bar的开盘价，_close i_ 是当前Tick的价格。

Range bars的吸引力在于它们承诺每个Bar的价格变动具有一致性。根据定义，每个Bar都代表了至少 R 的价格行程。这有助于标准化价格波动，使随后的分析（如波动率估算或模式识别）更加一致。

如果您想深入了解，请查阅此PDF。我个人喜欢它的方法：

Volume Centred Range Bars

636KB ∙ PDF file

下载

下面是 RangeBars 类如何实现此逻辑，它继承自 BaseBars：

class RangeBars(BaseBars):
    def __init__(self, threshold, batch_size=int(2e7)):
        super().__init__(None, batch_size)
        self.threshold = threshold

    def _check_bar(self, t, p, bars):
        if self.open is None:
            return
        if abs(self.close - self.open) >= self.threshold:
            bars.append([pd.to_datetime(t), self.stats['cum_ticks'],
                         self.open, self.high, self.low, self.close,
                         self.stats['cum_vol'], self.stats['cum_buy_vol'],
                         self.stats['cum_ticks'], self.stats['cum_dollar']])
            self.reset()

这里的核心是 _check_bar 方法。一旦价格从开盘点充分延伸，一个Bar就“诞生”了，然后这个过程会重置，等待下一个 R 大小的行情。当然，挑战在于选择一个合适的 R。如果太小，Bar会充斥着噪音；如果太大，则会错过关键的细微之处。

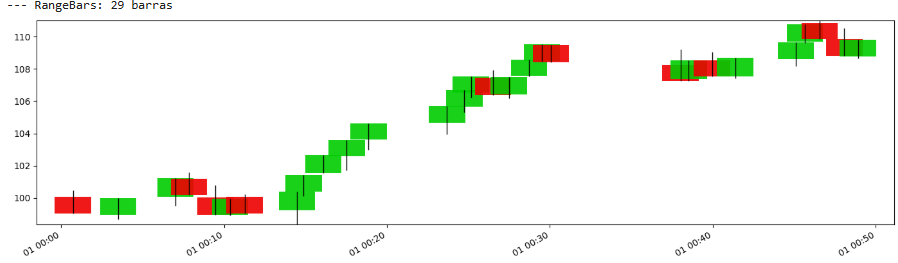
让我们来看：

在高波动性时期，许多这样的Bar会在短时间内形成，而在低波动性时期，则会在更长时间内形成较少的Bar。

优点：

每个Bar——理想情况下——代表着一致的价格波动量。这有助于规范价格行为。
在价格波动较大（波动性高）的时期会形成更多的Bar，而在平静时期则会形成更少的Bar，从而自然地将采样集中在活跃的市场区域。
固定的范围有时有助于识别由量化R定义的小型支撑位和阻力位。
通过要求最小价格变动，与平静市场中的时间Bar相比，一些较小、不那么重要的价格波动可能会被过滤掉。

缺点：

Range阈值 R 的选择至关重要，并且通常是数据特异性的——例如，与交易工具、市场条件相关。不恰当的 R 可能导致Bar过多（噪音），或Bar过少（丢失细节）。
Bar不会在固定时间间隔内闭合，这可能使得基于时间的分析或与基于时间指标的比较变得复杂。
如果市场波动剧烈，但整体价格变动频繁地来回穿越 R 阈值而未形成趋势，Range bar仍然可能生成许多导致反复止损（whipsaws）的信号。
如果价格进入一个远小于 R 的非常狭窄的盘整阶段，Bar的形成速度会大幅减慢或停止，可能错过微妙的积累/分配模式。

Renko bars（Renko Bar）

Renko bars（Renko Bar）起源于日本——类似于K线图（Candlesticks）——通过过滤掉微小的波动，提供了一种独特的方式来可视化价格变动和识别趋势。它们由预定义固定大小的“砖块” B 组成。只有当价格从上一个砖块的收盘价变动至少 B 时，才会添加一个新的砖块。如果价格沿当前方向变动 B，就会添加一个该颜色（例如，上涨为绿色，下跌为红色）的新砖块。关键在于，对于反转（即出现相反颜色的砖块），价格通常需要朝相反方向变动 2 B——一个 B 用于抵消当前砖块的方向，另一个 B 用于形成新的砖块。本示例代码实现了一个更简单的版本，即任何 B 的变动都会形成一个新的砖块。

条件是：每次自上一个砖块收盘以来累计价格变动 \(\Delta p\) 达到砖块大小 B 时，就会生成一个新的砖块。

\(\text{New brick when } |\text{current_price} – \text{last_brick_close}| \ge B\)

RenkoBars 类的实现：

class RenkoBars(BaseBars):
    def __init__(self, brick_size, batch_size=int(2e7)):
        self.last_close = None
        super().__init__(None, batch_size)
        self.brick_size = brick_size

    def reset(self):
        super().reset()
        if self.last_close is not None:
            self.open = self.high = self.low = self.close = self.last_close

    def _check_bar(self, t, p, bars):
        if self.last_close is None:
            self.last_close = p
        diff = p - self.last_close
        direction = np.sign(diff)
        num = int(abs(diff) // self.brick_size)
        for _ in range(num):
            o = self.last_close
            c = o + direction * self.brick_size
            bars.append([pd.to_datetime(t), self.stats['cum_ticks'],
                         o, max(o, c), min(o, c), c,
                         self.stats['cum_vol'], self.stats['cum_buy_vol'],
                         self.stats['cum_ticks'], self.stats['cum_dollar']])
            self.last_close = c
            super().reset()
            self.open = self.high = self.low = self.close = c

Renko bar擅长突出趋势——一系列相同颜色的砖块——以及支撑/阻力位。其整洁、清晰的外观令人耳目一新，但时间的抽象意味着两块连续的砖块可能在几秒或几小时内形成。 B 的选择再次至关重要。

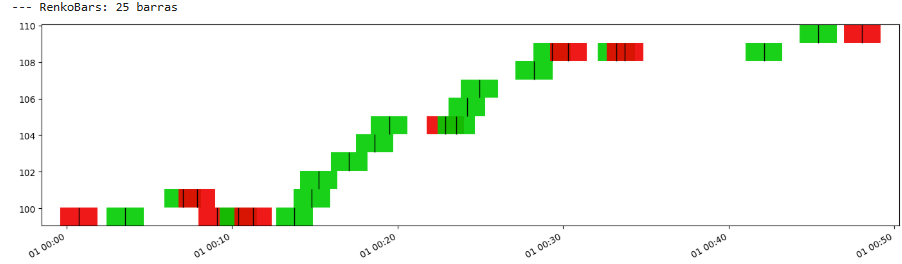
让我们来看：

正如你所看到的，Renko Bar和Range Bar非常相似。事实上，Renko Bar更“安静”。

优点：

Renko Bar通过过滤掉微小的价格波动，提供了一种非常清晰的趋势表示。一系列相同颜色的砖块是强烈的趋势信号。
通过仅关注至少大小为 B 的价格变动，Renko Bar有效地消除了噪音和逆趋势的小幅修正。
水平砖块线通常清晰地指示支撑位和阻力位。
统一的砖块大小和时间轴的移除使得Bar模式和趋势线非常明显。

缺点：

砖块大小 B 至关重要。太小，Bar会变得噪音大；太大，则会显著滞后，错过更精细的细节和进/出场点。
特别是经典的Renko Bar需要2 B 的反转才能形成，信号可能会延迟，导致入场或出场过晚。
Renko Bar不显示特定时间段内的确切高点和低点，只显示是否形成了砖块。所有不导致新砖块形成的价格行为都被忽略。
时间轴完全不规则。两个连续的砖块可能相隔几秒、几分钟甚至几小时形成，这使得基于时间的分析无法直接在Renko Bar上进行。
处理跳空（gaps）的方式可能有所不同，大的开盘跳空可能会扭曲初始砖块的形成。

Filter bars（过滤Bar）

Filter bars（过滤Bar），有时也称为固定百分比Bar或对数价格Bar——尽管后者更具体——旨在当价格相对于基准价格 _p base_ 移动一定百分比 θ 时形成新的Bar。这个 _p base_ 通常是上一个形成的Bar的收盘价或当前Bar的开盘价。

条件是：

\(\text{close when}\quad \frac{\lvert p_i – p_{\mathrm{base}}\rvert}{p_{\mathrm{base}}} \ge \theta \)

其中 _p i_ 是当前价格。

这类Bar很有趣，因为固定的百分比变动意味着不同的绝对价格变化，具体取决于当前价格水平。10美元时1%的变动是0.10美元，而在1000美元时则是10美元。这可能更适用于波动率随价格变化的资产。

FilterBars 的实现：

class FilterBars(BaseBars):
    def __init__(self, threshold_pct, batch_size=int(2e7)):
        super().__init__(None, batch_size)
        self.threshold_pct = threshold_pct
        self.base = None

    def reset(self):
        super().reset()
        self.base = None

    def _check_bar(self, t, p, bars):
        if self.base is None:
            self.base = p
        move = abs(p - self.base) / self.base if self.base != 0 else 0
        if move >= self.threshold_pct:
            bars.append([pd.to_datetime(t), self.stats['cum_ticks'],
                         self.open, self.high, self.low, p,
                         self.stats['cum_vol'], self.stats['cum_buy_vol'],
                         self.stats['cum_ticks'], self.stats['cum_dollar']])
            self.reset()

Filter Bar动态地调整形成新Bar所需的绝对价格变化，这使得它们在不同价格状态或价格幅度不同的资产之间可能更具稳健性。关键障碍仍然是 θ 的明智选择。

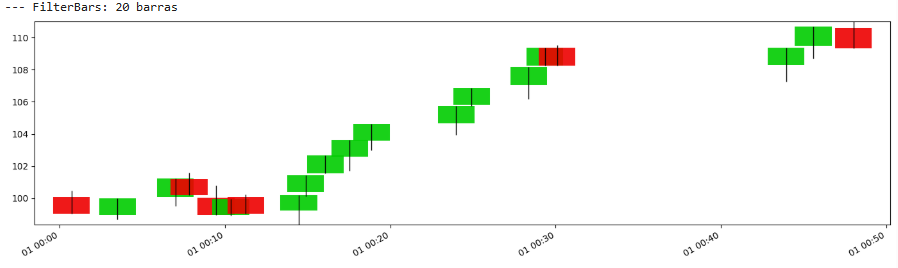
让我们来绘制它：

再一次，与之前的Bar没有太大区别。

优点：

固定的百分比变动解释了1美元的变动对于10美元的股票比对于1000美元的股票更为显著的事实。这使得Bar在不同价格水平之间或对于波动性不同的资产具有可比性。
每个Bar代表相似的百分比变化，这可能对某些专注于相对价值或基于对数收益率（log-return）信号的策略更有意义。
随着价格上涨，形成新Bar所需的绝对价格变化也会增加——反之亦然。换句话说，当价格较高时，每个Bar需要更大的美元金额变动才能触发。

缺点：

百分比阈值 θ 的选择至关重要，并且需要仔细校准。
行为可能会因 _p base_ 是Bar的开盘价、前一个收盘价还是其他参考点而产生细微变化。
与其他信息驱动型Bar一样，它们不会在固定时间间隔内形成。
如果 θ 设置得适合较高价格水平，对于价格非常低、波动性大的资产，它可能仍然太小，导致形成许多Bar。相反，如果为低价资产设置，它在高价位时可能不够敏感。
如果 _p base_ 非常小，则极端敏感。

Volatility bars（波动率Bar）

Volatility bars（波动率Bar）采用更直接的方法与市场状况同步。当在特定回溯窗口 W （通常是Tick或时间，但为了与Bar类型一致，通常指Tick）观察到的波动率超过预设的波动率阈值 σ 时，就会形成一个新的Bar。

条件是：

\(\text{compute }s = \operatorname{stdev}\bigl(\{\,p_{i-W+1}, \ldots, p_{i}\,\}\bigr) \quad \text{close if }s \ge \sigma \)

此处，s 是在最近 W 个Tick内的价格标准差。

这种方法在直觉上很有吸引力，因为它直接适应了市场行为最关键的方面之一。然而，它引入了两个需要调整的参数：W 和 σ。 W 的选择决定了波动率估算的响应性，而 σ 则设定了Bar创建的敏感度。

VolatilityBars 的实现：

class VolatilityBars(BaseBars):
    def __init__(self, vol_threshold, window, batch_size=int(2e7)):
        # initialize window first so reset can clear it
        self.window = deque(maxlen=window)
        super().__init__(None, batch_size)
        self.vol_threshold = vol_threshold

    def reset(self):
        super().reset()
        self.window.clear()

    def _check_bar(self, t, p, bars):
        self.window.append(p)
        if len(self.window) == self.window.maxlen:
            vol = float(np.std(np.array(self.window)))
            if vol >= self.vol_threshold:
                bars.append([pd.to_datetime(t), self.stats['cum_ticks'],
                             self.open, self.high, self.low, self.close,
                             self.stats['cum_vol'], self.stats['cum_buy_vol'],
                             self.stats['cum_ticks'], self.stats['cum_dollar']])
                self.reset()

波动率Bar直观上很有吸引力，因为它们直接适应了市场行为最关键的某个方面。然而，它们引入了两个需要调整的参数： W 和 σ。W 的选择决定了波动率估计的响应性，而 σ 则设置了Bar创建的敏感度。

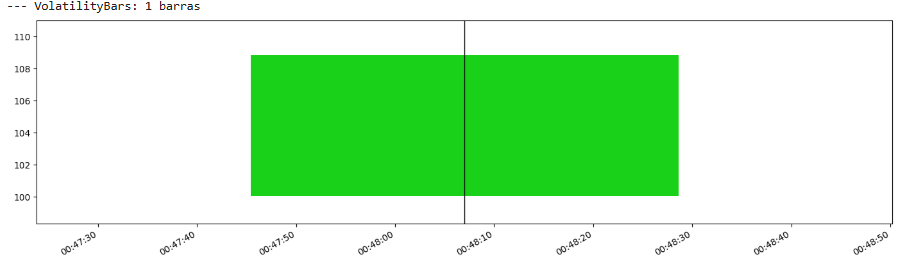
让我们来看：

等等，怎么回事！？兄弟们，数据量有点少啊，这个Bar效果不佳…

优点：

市场波动时Bar自然形成得更快，平静时则更慢。这使采样与市场“事件性”或风险保持一致。
每个Bar都试图捕捉相似量的已实现波动率或意想不到的变化。
可以形成一个Bar序列，其中每个Bar的Tick数量或持续时间等量化属性更具统计学优势，便于建模。
对于在高波动率与低波动率状态下需要不同行为的策略非常有用。

缺点：

需要设置波动率计算的回溯窗口 W 和波动率阈值 σ。这增加了优化复杂性和过度拟合的风险。
虽然标准差很常见，但也可以使用其他波动率估算器，每种都有其自身的特性和影响。
回溯窗口 W 会导致波动率估算存在一定滞后。较短的窗口响应更快但噪音更大；较长的窗口更平滑但反应较慢。
与其他信息驱动型Bar共通的缺点是，此外，它采样速度过慢。

好的，Range、Renko、Filter和Volatility bars所提供的解决方案很有趣。它们解决了基于时间采样无法区分市场活跃期和平静期的核心问题。

通过设计，这些Bar旨在实现更稳定的统计特性——更接近独立同分布（IID）、收益的正态性。这使得统计学习模型（statistical learning models）和风险管理框架能更可靠地应用，因为这些框架往往带有原始时间序列数据所违反的假设。异方差诅咒（curse of heteroskedasticity）即使未完全解除，也得到了显著缓解。
算法不再被动地按固定时间间隔监听，而是进行动态对话。它们在市场“坚定发声”时进行采样。这种适应性可以促使更快地应对新出现的趋势，并减少在盘整期间被反复止损（whipsawed）的风险。这就像是定期体检和紧急响应系统之间的区别。
基于这些更统一的信息单元设计的特征——例如，N个信息Bar的动量、N个信息Bar的波动率——可以比基于时间Bar构建的特征更具稳健性，并且在不同的市场状态下更具可比性，因为时间Bar封装的信息量差异巨大。

这里的结论是：

没有普遍意义上的“最佳”Bar类型。
最佳选择取决于特定的资产类别、交易策略的时间范围和逻辑，以及市场微观结构。
趋势跟踪策略可能偏爱Renko Bar的清晰性，而突破策略可能更倾向于Range Bar或Volatility bars。

让我们从视觉上进行最终比较：

除了采样速度极慢的Volatility bar外，其余的Bar至少在视觉上产生了相当相似的结果。在下一期——这是本系列的第2/3部分——我们将从统计学角度深入探讨。

好的，各位！今天表现非常出色！现在是时候“下班”了。保持好奇，保持无限，保持量化思维！

P.S.：到目前为止，您会选择哪种Bar呢？

原文链接

数据：区间Bar、Renko Bar、过滤Bar和波动率Bar [Trading the Breaking]

数据：Range、Renko、Filter和Volatility bars [+代码示例]

金融Bar之二

目录：

引言

时间Bar的风险与局限性

信息驱动型Bar介绍

Range bars（区间Bar）

Renko bars（Renko Bar）

Filter bars（过滤Bar）

Volatility bars（波动率Bar）

评论

发表回复 取消回复

更多文章

波动性的波动：VVIX的启示 [相对价值套利]

解读美国市场的隔夜收益 [Joachim Klement]

波动性中的波动性：VVIX的启示 [相对价值套利]

解析美股隔夜收益 [Joachim Klement]

发表回复取消回复